Paradoxes

Paradoxes are entertaining riddles that makes education fun. I've therefore decided to use one of Zeno's paradoxes to illustrate some interesting aspects of mathematics for my son. Starting with some basic maths related to infinite sequences, we see that not all such sequences end up with infinity. An infinity of consecutively smaller numbers end up with a finite number.

Many paradoxes can be solved with this bit of insight. When we deal with motion by dividing space into increasingly smaller parts, we divide time into correspondingly smaller parts. What we end up with is not an infinite time, but a finite time. The paradox disappears, because we see that all that is said is that a finite distance will be traversed by a moving body in a finite amount of time.

However, there is nevertheless something fundamentally interesting about these paradoxes. They seem to indicate that infinitesimally small subdivisions do not exist. Both space and time appear to be atomic in nature, as suggested in my aether physics. At some point, subdivision is no longer possible, and the full length of atomic space and time must be traversed, rendering the paradox invalid.

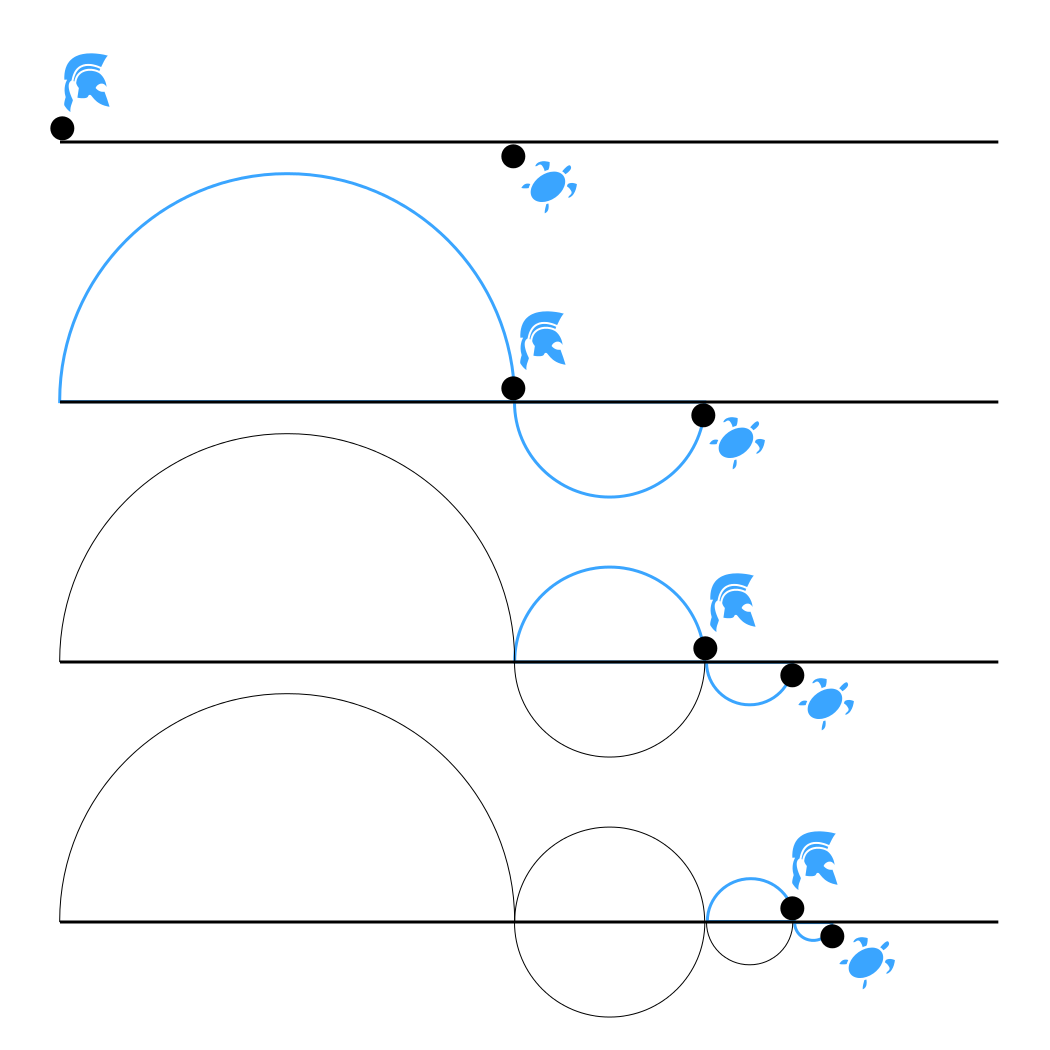Achilles and the tortoise

By Martin Grandjean - Own work, CC BY-SA 4.0, Link